【心理学統計法】こころをデータにしてわかりやすく伝えることが出来ます

1-2.認定心理士

2024.05.04 2024.02.12

この記事は約16分で読めます。

毎度です！

人生山あり谷ありで、アラフィフで大手前大学の通信課程の現役通信女子？大生の森﨑さくらです。

3年前に大手前大学に入学し、認定心理士と日本語教師を目指しています。

認定心理士の資格を取得するには、統計は必須です。

認定心理士に必要であり、スクーリングの「心理学実験演習A・B」を受ける前に受講しときましょうなんてシラバスにも書いてます。

※先修条件「心理学統計法」「心理学研究法」の学習内容を理解していることを要する。
出典：大手前大学通信教育部　シラバス「心理学実験演習AB」より

認定心理士を目指すならば、逃げることはできません。

これは、やるしかない‥ってことで、昨年度も履修登録はしたのですが、逃げてしまいました。

そして、いよいよ今年度は、統計に力を入れるぞっと決めて、1クール目から履修登録していました。

それが、第4クールまでかかってしまいました。

やっと試験を受けることができました！

まだ、合格はしていませんが、出来ることはやりました！

この記事は

●アラフィフで学びなおしをした社会人通信大学生の体験ブログです。

●認定心理士と日本語教師を目指しています。

●通信制大学ってとってもすんばらしいと思っている人がここにおります。

●読んでも参考にならないただの備忘録ですが、一緒にがんばっていただけると励みになります。

【心理学統計法】確認テストの注意点
心理学統計法で使うエクセルの関数
便利なピボットテーブルを使いこなそう
心理学統計法で重要な名称
ピーチ（P値）って？
そもそも帰無仮説とは？
二元要因分散分析
単位修得試験対策
【心理学統計法】こころをデータにしてわかりやすく伝えることが出来ますのまとめ

【心理学統計法】確認テストの注意点

さて、当たり前のことですが、「四捨五入して小数第2位まで」などをきっちり守りましょう。

例えば、答えが、「30.298」だとします。

「小数点第2位まで求めなさい。」の場合は、答えは「30.30」ですよね。

おバカな私は、ここを「30.3」としてしまって確認テストを間違えてしまいます。。。。

この失敗は、回が進んでも続いていて辛いです。。

悲しい・・・

確認テストは、10問くらいあります。

たった小数点以下の数を間違えただけ（そんな風に軽く考えているから何度も同じミスをする）で、また、やり直しです。。。

ぐったりしますので、テストを終られたら、提出する前に小数点以下の数が間違っていないか確認しましょう。（こんなミス、私くらいでしょうか・・・）

心理学統計法で使うエクセルの関数

エクセルは必須です。

関数をガシガシ使うしかありません。

使った関数や計算式をまとめてみました！

求めたいもの	関数	使用例
平均値（μ）	AVERAGE	=AVERAGE(C3:C49)
中央値	MEDIAN	=MEDIAN(B3:B24)
最頻値	MODE	=MODE(B3:B24)
最大値	MAX	=MAX($D$2:$D$157)
最小値	MIN	=MIN($D$2:$D$157)
階級の度数（3以上6未満の数）	COUNTIFS	=COUNTIFS($B$3:$B$24,”>=3″,$B$3:$B$24,”<6″)
分散	VAR.P	=VAR.P(B2:B10)
標準偏差（σ）	STDEV.P	=STDEV.P(C3:C49)
5パーセンタイル値	PERCENTILE.INC	=PERCENTILE.INC($C$2:$C$35,0.05)
30パーセンタイル値	PERCENTILE.INC	=PERCENTILE.INC($C$2:$C$35,0.3)
50パーセンタイル値	PERCENTILE.INC	=PERCENTILE.INC($C$2:$C$35,0.5)
70パーセンタイル値	PERCENTILE.INC	=PERCENTILE.INC($C$2:$C$35,0.7)
95パーセンタイル値	PERCENTILE.INC	=PERCENTILE.INC($C$2:$C$35,0.95)
相関係数	CORREL	=CORREL(B3:B14,C3:C14)
共分散	COVARIANCE.P	=COVARIANCE.P(B3:B14,C3:C14)
偏相関係数		=(G3-H3H4)/(((1-H3^2)^0.5)((1-H4^2)^0.5))
不偏分散 (推測統計）	VAR.S	=VAR.S(C3:C49)
不偏標準偏差 (推測統計）	STDEV.Ｓ	=STDEV.Ｓ(C3:C49)
Ｐ値	T.DIST.2T
期待値とのズレ		＝（実測値－期待値）²/期待値
自由度	（期待値セルの）	＝（行数-1）*（列数-1）
F検定	F.TEST	=F.TEST(E34:E38,E39:E42)
t検定	対応のあるｔ検定	データ➡データ分析➡「t検定：一対の標本による平均の検定」
t検定	対応のないｔ検定	データ➡データ分析➡「t検定：等分散を仮定した2標本による検定」
母分散	不偏分散	母平均の推定値である標本平均の標準偏差
標準誤差	標本平均の標準偏差	＝母分散/ｎ数＾0.5　又は、＝不偏分散/ｎ数＾0.5
検定測定量ｔ値		＝差の平均/標準誤差
F値	検定統計量F値	＝平均平方（MS）/平均平方（MS）の誤差

便利なピボットテーブルを使いこなそう

ピボットテーブルは、クロス集計の時などに使用します。

例えば、アンケートなどで、「知っている」「しらない」「わからない」等を答えてもらいます。

そうすると、その数を集計しないといけないですよね。

10個くらいなら、数えることが出来ます。

しかし、100個1000個などある場合、集計が大変です。

そこで、エクセルの「ピボットテーブル」を使います。

これが便利なのです。

マスターしましょう！

ピボットテーブルの作り方はコチラから

エクセル小技：行を列に入れ替える

コピーした表を行と列を入れ替えてペーストすることが出来ます。

貼り付ける際に、下図の黄色いところをクリックします

心理学統計法で重要な名称

力尽きながら、名称を集めてみました。

名称
中央値	順番に並べて中央の値	2個あったら平均値
範囲	最大値と最小値の差	＝MAX関数で求めた数値-MIN関数で求めた数値
偏差	データの値－平均値
平均偏差	偏差の平均値	－は+にする
分散	偏差＾2の平均値	平均平方（MS)
標準偏差（σ）	分散＾0.5（√ﾙｰﾄ）	σ（シグマ）
標準得点	（データの値－平均値）/標準偏差	Z値・Z得点
偏差値	50＋（標準得点）*10
変動係数	標準偏差/平均値	データ同士のばらつきを相対的に評価するための値
パーセンタイル	並べたデータの小さい方から何％目	中央値が50パーセントタイル値
箱ひげ図	データを1/4にして五数要約を可視化	五数要約（パーセンタイル）：最小値・第1四分位数（25％）・中央値（50％）・第3四分位数（75％）・最大
変数	データの値
制御変数		実験結果への影響を除外するための要因
相関係数		変数間の関係の強さと方向を測る指標
偏相関係数	疑似相関を調べる	別の要因があるかも
帰無仮説	否定的な仮説	背理法的　「○○ではない」
P値	確率	帰無仮説を棄却するか否かの基準となる確率
有意水準	棄却の目安	ｐ値の基準
F検定	2標本の分散が等しいか	2つのグループの母分散によってt検定の計算が変わる
t検定	対応のあるｔ検定	同じ標本
t検定	対応のないｔ検定	違う標本
F値	検定統計量F値	群間と群内のばらつき比較、平均差異の評価
独立変数	原因	実験者が操作できる要因
従属変数	結果	影響される結果

ピーチ（P値）って？

はい、これは桃です！

はい、こちらは航空機です。

心理学統計法を学ぶと、とにかく「ピーチ・ピーチ」とよく聞います。

どうやら、重重要な用語だそうです。

かわいい名前なんだけどね・・・

わかんないのよ・・意味が・・・

p値＝有意確率
p値のｐ＝Probability（確率）の頭文字

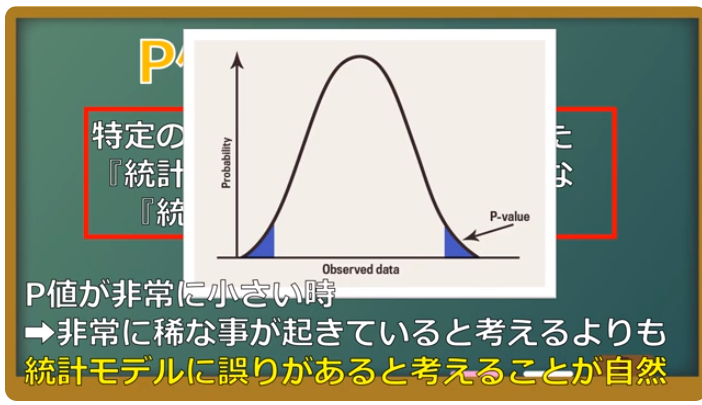
上記「検定統計量の分布図」の青い部分が、P値だそうです。

p値が0.05より小さい時＝統計モデルに誤りがある＝帰無仮説の誤り

つまり、、、

P値が5％より小さい時に帰無仮説を棄却する

となります。

「有意水準が0.05でP値が0.03だったので有意である」

吉田美和さん

「有意になる基準が5％で、p値が3％だったので、有意である」という意味だね。

有意水準とは、有意となる基準の数値ことです。

有意とは、意味が有ることです。

体重が気になるお年頃

P値の考え方について、ざっくりと私なりの解釈をお伝えします。

体重で言えば、ＷＨＯ（世界保健機構）の基準では、BMIが30以上の場合は、肥満としているそうです。（参照元：ｅ–ヘルスネット）

この、「30」が有意水準であって、30より大きいと肥満ということになります、、、

例えば、わたしはBMIが「31」だったとします。

有意水準の「30」を超えているので有意になります。

帰無仮説：私は肥満ではない

対立仮説：私は肥満である

さくら

有意水準を超えているので、肥満ではないという帰無仮説を棄却し、肥満であるという対立仮説を採択します。

合ってますか？笑

いつか、ちゃんと理解したいです。。。（勉強中です）

そもそも帰無仮説とは？

帰無する仮説＝無に帰る仮説＝否定したい方の仮説

そして

帰無仮説を立てるとは、実際に思っている方とは逆の仮説として立てること

帰無仮説を棄却するとは、否定したい仮説をやっぱり違うよねと間違いと確定する。

さくら

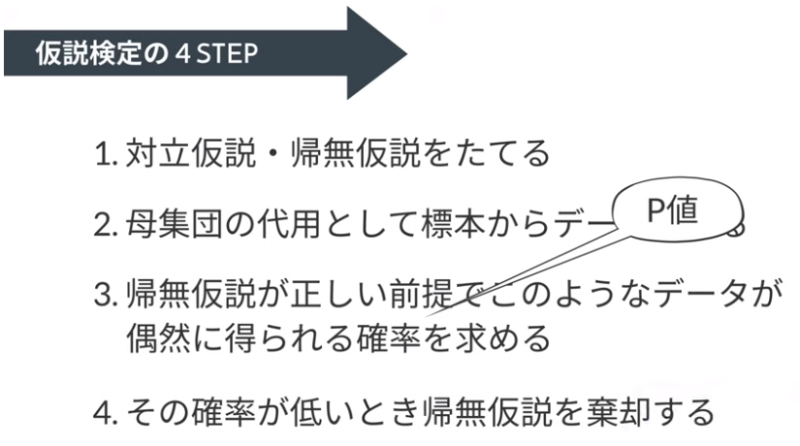
そんな風に理解して、試験を受けました。。。

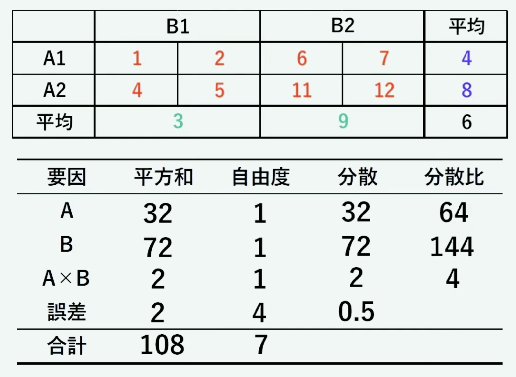
二元要因分散分析

主効果と交互作用・・・

こちらも、エクセルのデータから簡単に分散分析ができます。

分析表のp値を見て、0.05以下の場合は、帰無仮説を棄却するそうです。

出典：**［解答テクニック］二元配置分散分析の肝である交互作用。これでもう間違えない！**

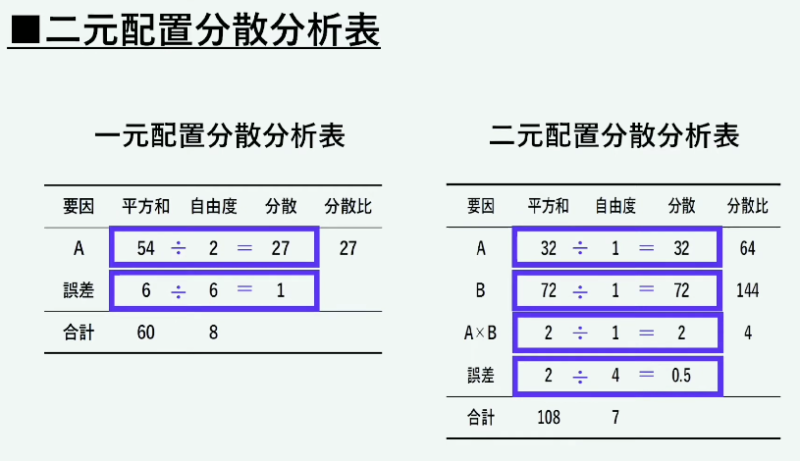
分散比＝各要因の分散/誤差分散・・・要因Aの分散比＝32/0.5＝64

簡単に分散分析ができる。。。

といいましたが、解釈が難しく、ここから読みとくことが出来ない。。。( ；∀；)

単位修得試験対策

それを言っちゃぁーおしまいよぉ～なんですが、「この調査にはこの統計方法がいい」ってわかることが大切だと思います。

そして、読み解けること。

私は、この部分、いわゆるキモが理解できてなかったと思います。

エクセルを使った計算方法を習得しようと頑張っていました。

カイ二乗・回帰分析・分散分析。。。

ややこしい、でもとにかく、やるしかないっ！・・・で、乗り越えました。

対策は、諦めないことですかね。。（白目）